Description
Implementing quick hull in computational design:
Quickhull is a method of computing the convex hull of a finite set of points in the plane. It uses a divide and conquer approach similar to that of quicksort, from which its name derives. Its average case complexity is considered to be Θ(n * log(n)), whereas in the worst case it takes O(n2) (quadratic).


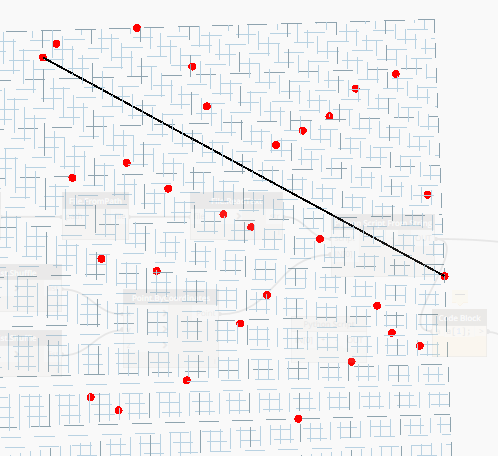
Starting Point
From the set of points we determine 2 points. First with the minimum value of X coordinate and the other with the maximum value of X coordinate. We connect the points (min to max) and respect the order of connecting the points through out the process in order to get correct filtering when determining left from right points.

def min_max_x(pts):
minX = pts[0].X
maxX = pts[0].X
minXPoint = pts[0]
maxXPoint = pts[0]
for pt in pts:
if pt.X < minX:
minX = pt.X
minXPoint = pt
if pt.X > maxX:
maxX = pt.X
maxXPoint = pt
return minXPoint, maxXPoint
Helpers
A point in 2d can be classified as being on the right side or left side by using the following algorithm : (see see Point on line side:
def PointSide(point, line):
sp = line.StartPoint
ep = line.EndPoint
d = (point.X - sp.X) * (ep.Y - sp.Y) - (point.Y - sp.Y)*(ep.X - sp.X)
if d > 0:
return 1
elif d == 0:
return 0
else:
return -1
def PointsRightSide(points, line):
ret = []
for pt in points:
if (PointSide(pt, line)) > 0:
ret.append(pt)
return ret
def PointsLeftSide(points, line):
ret = []
for pt in points:
if (PointSide(pt, line)) < 0:
ret.append(pt)
return ret
For this line we will use the functions above to create 2 sets of points, on for each side of the line
def quick(pts):
#determining points with min and max X coordinate
minXPoint, maxXPoint = min_max_x(pts)
#creating line between these points
lineMinMaxX = Line.ByStartPointEndPoint(minXPoint, maxXPoint)
#determining points on right and left side
ptsRight = PointsRightSide(pts, lineMinMaxX)
ptsLeft = PointsLeftSide(pts, lineMinMaxX)
return lineMinMaxX, ptsRight
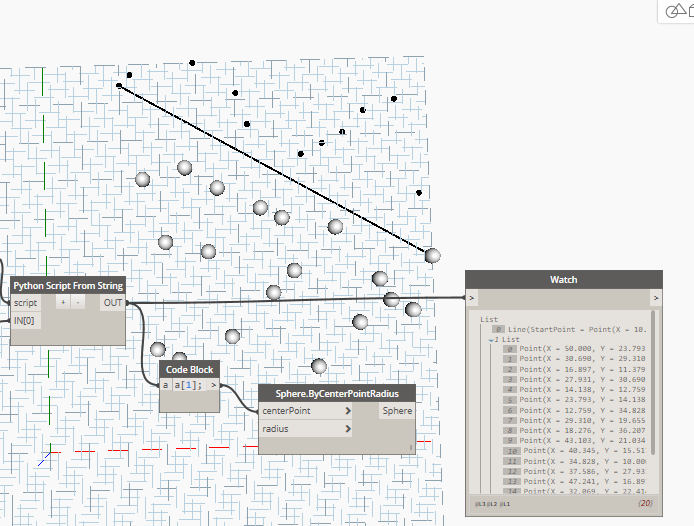

Short workflow description
Get the farthest point from the line (see the cyan line connecting the yellow line). Create the triangle and remove points whithin. For this we will use Dynamo containment test. Further on for each yellow line we will check if there are any points on the outside (on the right or left) and reiterate this process until there are no points on the outside.
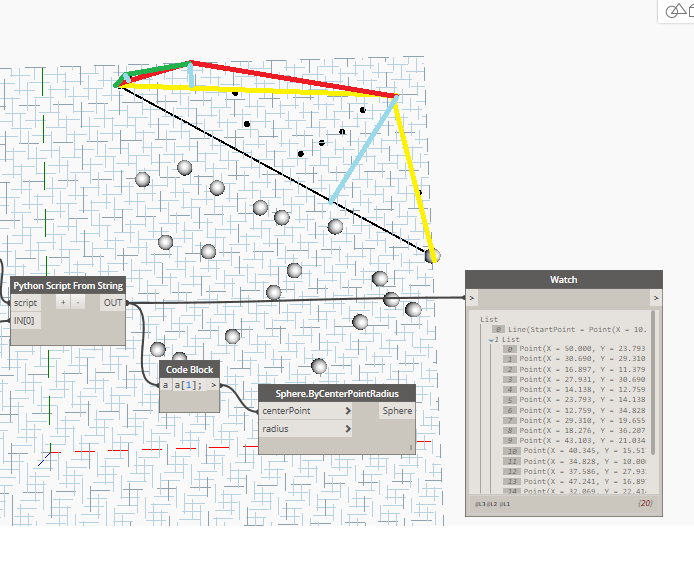

Components
def PointFarthest(points, line):
if len(points) == 0:
return None
far = points[0]
for pt in points:
if pt.DistanceTo(line) > far.DistanceTo(line):
far = pt
return far;
def MainTriangles(point, line):
if point is None:
return None
return Polygon.ByPoints([line.StartPoint, point, line.EndPoint])
def GetRestOfPoints(polygon, points):
if polygon is None:
return None
restOfPoints = []
for point in points:
if not Polygon.ContainmentTest(polygon, point) and not polygon.DoesIntersect(point):
restOfPoints.append(point)
return restOfPoints
An example of removing inside points below:
def quick(pts):
#determining points with min and max X coordinate
minXPoint, maxXPoint = min_max_x(pts)
#creating line between these points
lineMinMaxX = Line.ByStartPointEndPoint(minXPoint, maxXPoint)
#determining points on right and left side
ptsRight = PointsRightSide(pts, lineMinMaxX)
ptsLeft = PointsLeftSide(pts, lineMinMaxX)
#determining farthers points from line
farPointRight = PointFarthest(ptsRight, lineMinMaxX)
farPointLeft = PointFarthest(ptsLeft, lineMinMaxX)
#main triangles
mainTriangleLeft = MainTriangles(farPointLeft, lineMinMaxX)
mainTriangleRight = MainTriangles(farPointRight, lineMinMaxX)
#rest of points
restOfPointsLeft = GetRestOfPoints(mainTriangleLeft, ptsLeft)
restOfPointsRight = GetRestOfPoints(mainTriangleRight, ptsRight)
return lineMinMaxX, mainTriangleRight, restOfPointsRight


Complete solution
The complete code with recursive implementation:
import clr
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *
def min_max_x(pts):
minX = pts[0].X
maxX = pts[0].X
minXPoint = pts[0]
maxXPoint = pts[0]
for pt in pts:
if pt.X < minX:
minX = pt.X
minXPoint = pt
if pt.X > maxX:
maxX = pt.X
maxXPoint = pt
return minXPoint, maxXPoint
def PointSide(point, line):
sp = line.StartPoint
ep = line.EndPoint
d = (point.X - sp.X) * (ep.Y - sp.Y) - (point.Y - sp.Y)*(ep.X - sp.X)
if d > 0:
return 1
elif d == 0:
return 0
else:
return -1
def PointsRightSide(points, line):
ret = []
for pt in points:
if (PointSide(pt, line)) > 0:
ret.append(pt)
return ret
def PointsLeftSide(points, line):
ret = []
for pt in points:
if (PointSide(pt, line)) < 0:
ret.append(pt)
return ret
def PointFarthest(points, line):
if len(points) == 0:
return None
far = points[0]
for pt in points:
if pt.DistanceTo(line) > far.DistanceTo(line):
far = pt
return far;
def MainTriangles(point, line):
if point is None:
return None
return Polygon.ByPoints([line.StartPoint, point, line.EndPoint])
def GetRestOfPoints(polygon, points):
if polygon is None:
return None
restOfPoints = []
for point in points:
if not Polygon.ContainmentTest(polygon, point) and not polygon.DoesIntersect(point):
restOfPoints.append(point)
return restOfPoints
def GetNextPointRight(line, points):
ptsRight = PointsRightSide(points, line)
farPointRight = PointFarthest(ptsRight, line)
mainTriangleRight = MainTriangles(farPointRight, line)
restOfPoints = GetRestOfPoints(mainTriangleRight, ptsRight)
if len(ptsRight) == 0:
return line
r1 = GetNextPointRight(Line.ByStartPointEndPoint(line.StartPoint, farPointRight), restOfPoints)
r2 = GetNextPointRight(Line.ByStartPointEndPoint(farPointRight, line.EndPoint), restOfPoints)
return [r1, r2]
def GetNextPointLeft(line, points):
ptsRight = PointsLeftSide(points, line)
farPointRight = PointFarthest(ptsRight, line)
mainTriangleRight = MainTriangles(farPointRight, line)
restOfPoints = GetRestOfPoints(mainTriangleRight, ptsRight)
if len(ptsRight) == 0:
return line
r1 = GetNextPointLeft(Line.ByStartPointEndPoint(line.StartPoint, farPointRight), restOfPoints)
r2 = GetNextPointLeft(Line.ByStartPointEndPoint(farPointRight, line.EndPoint), restOfPoints)
return [r1, r2]
def quick(pts):
#determining points with min and max X coordinate
minXPoint, maxXPoint = min_max_x(pts)
#creating line between these points
lineMinMaxX = Line.ByStartPointEndPoint(minXPoint, maxXPoint)
#determining points on right and left side
ptsRight = PointsRightSide(pts, lineMinMaxX)
ptsLeft = PointsLeftSide(pts, lineMinMaxX)
resultRight = GetNextPointRight(lineMinMaxX, ptsRight)
resultLeft = GetNextPointLeft(lineMinMaxX, ptsLeft)
return resultLeft, resultRight
OUT = quick(IN[0])