Dynamo Python – Distribute lines along curve

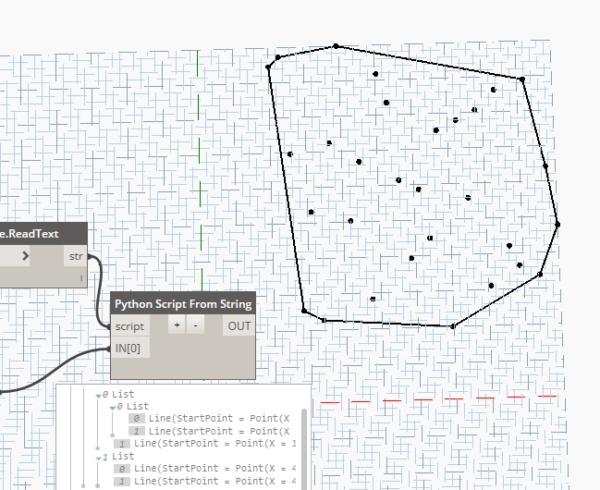
Perhaps not the most useful application in Dynamo however a pretty cool exercise. Line distribution along a polycurve is especially important when you want to determine the curvature degree along the curve for road projects. This exercise will open a door in that direction.

Utilitary class (handles list checks and list unwrapping)

import clr
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *
import re
#utilitary

class utils:
	ul = [];
	def __init__(self):
		self.ul = [];
	def isIterable(self, unit):
		t1 = t2 = False;
		if(isinstance(unit, (tuple, set, list, dict))):
			t1 = True;
		if(hasattr(unit, "__iter__")):
			iterstr = str(unit.__iter__());
			if(re.search("System.Array", iterstr)):
				t2 = True;
		return (t1 or t2);
	def UnwrapList(self, list):
		self.ul = [];
		if(self.isIterable(list)):	
			self.UnwrapL(list);
			return self.ul;
		else:
			return list;
			
	def UnwrapL(self, unit):
		if(self.isIterable(unit)):
			for item in unit:
				self.UnwrapL(item);
		else:
			self.ul.append(unit);

ut = utils();

Functions used to calculate and create the lines directions, lengths and positions

#main functions

def getPerpVector(curve, parameter):
	TP = curve.TangentAtParameter(parameter);
	VT = Vector.Rotate(TP, Vector.ZAxis(), 90);
	return VT;
	
def getPerpLine(curve, parameter, length):
	perpVector = getPerpVector(curve, parameter);
	pointAtParam = curve.PointAtParameter(parameter);
	L = Line.ByStartPointDirectionLength(pointAtParam, perpVector, length);
	return L;

def composeLNF(Arc_Length, Arc_Parameters):
	ALU = Arc_Length;
	APU = Arc_Parameters; 
	ALU_L = len(ALU);
	APU_L = len(APU);
	N = [];
	P = [];
	for index1 in range(ALU_L - 1):
		N.append([]);
		LLeft = ALU[index1];
		LRight = ALU[index1 + 1];
		for index2 in range(APU_L-1):
			steper = float(index2) / (APU_L-1);
			Dist = float(LLeft) + (float(LRight) - LLeft) * steper;
			N[index1].append(Dist);
	N.append(ALU[ALU_L - 1])
	
	P = ut.UnwrapList(N);
	P_L = len(P);
	segment = float(P_L) / APU_L;
	LE = [];
	#return segment
	for index3 in range(APU_L):
		newIndex = int(float(P_L-1) / (APU_L-1) * index3)
		resIndex = int((index3 * segment));
		LE.append(P[newIndex]);
	return LE;

Because the input can be jagged (varying size) we need a function to deal with these inputs and it has to be recursive:

#iteration along various array sizes.
def returnElements(Arc_Curves, Arc_Parameters, Lengths):
	if(isinstance(Arc_Curves, (list, tuple))):
		retList = [];
		for Arc_Curve in Arc_Curves:
			retList.append(returnElements(Arc_Curve, Arc_Parameters, Lengths));
		return retList;
	elif(isinstance(Arc_Parameters, (list, tuple))):
		retList = [];
		for index, Arc_Parameter in enumerate(Arc_Parameters):
			try:
				retList.append(getPerpLine(Arc_Curves, Arc_Parameter, Lengths[index]));
			except:
				retList.append(False);
		return retList;
	else:
		return getPerpLine(Arc_Curves, Arc_Parameters, Lengths)

These final lines of code will create the lengths for all the parameters given as input. E.G. You can provide 100 parameters (from 0 to 1) and 3 lengths for the curves. These lengths will be evenly distributed from the beginning to the end of the main curve, and for all the input parameters a proper length is assigned.

#input data assignment 
		
Arc_Curves = IN[0];
Arc_Parameters = IN[1];
Arc_Length = IN[2];

#input data clean up
if(ut.isIterable(Arc_Parameters)):
	Arc_Parameters = ut.UnwrapList(Arc_Parameters);
	if(ut.isIterable(Arc_Length)):
		Arc_Length = ut.UnwrapList(Arc_Length);
		Lengths = composeLNF(Arc_Length, Arc_Parameters);
	else:
		Arc_Length = [Arc_Length];
		Lengths = composeLNF(Arc_Length, Arc_Parameters);
else:
	if(ut.isIterable(Arc_Length)):
		Lengths = False;
	else:
		Lengths = Arc_Length

At the end, create the output, wrap it all under a custom node and use it as below:

#executing

Result = returnElements(Arc_Curves, Arc_Parameters, Lengths);

OUT = Result, Lengths