C# Projecting a point onto a line by a direction

There are multiple ways to determine the projected point onto a line, my personal approach uses the parametric equation of lines.

Considering the following : We have a line defined by points A(Xa, Ya) and B(Xb, Yb), we have an arbitrary point C(Xc, Yc), a vector V(Xv, Yv) and we want to determine the coordinates of point D(Xd, Yd) representing the projected point from C to line AB.

The parametric equation represents the function of the line an it’s a factor of t where t represents the relative position of a point on the line. For our line we have the following equations:

From these 2 equations we can determine a1 and b1 by substituding t with 1. The parameter “t” will map a point on a line with values from 0 to 1, where a value of 0 represents the start point and a value of 1 represents the end point.

By considering t = 1 we must also consider that xt and yt belong to the end point. Therefore :

The goal is to find 2 parametric equations of 2 lines, and find the common value of t between them. From the the point C and the vector V we will create a line. We do so by determining translating C with a small distance in the direction of V. The new point C1 will be the end point of line CC1

Now that we have our second line defined, we can also determine it’s coefficients for the parametric equation:

We have 2 lines and 2 parametric equations (to rule them all!). The point that we have to determine has a different “t” for each line but the same “xt” and “”yt”

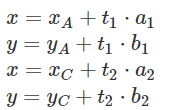
Solving these equations leads us to the parameter “t” of the projected point on line AB:

public static double ParameterAtPoint(Line2D line2D, Point2D point2D)
{
    //determine line coefficients
    double A = line2D.EndPoint.X - line2D.StartPoint.X;
    //double B = line2D.EndPoint.Y - line2D.StartPoint.Y;
    double t = (point2D.X - line2D.StartPoint.X) / A;

    return t;
}
public static Point2D getProjectedPointOnLine(Point2D toProject, Line2D line2D, Vector2D direction)
{
    Point2D otherPoint = new Point2D(toProject.X + direction.X, toProject.Y + direction.Y);

    double Al = line2D.EndPoint.X - line2D.StartPoint.X;
    double Bl = line2D.EndPoint.Y - line2D.StartPoint.Y;
    double Apl = otherPoint.X - toProject.X;
    double Bpl = otherPoint.Y - toProject.Y;
    //t parameter on the projection line
    double t2 = ((toProject.Y - line2D.StartPoint.Y) * Al - (toProject.X - line2D.StartPoint.X) * Bl) / (Apl * Bl - Al * Bpl);
    //t parameter value on the input line
    double t1 = ((line2D.StartPoint.Y - toProject.Y) * Apl - (line2D.StartPoint.X - toProject.X) * Bpl) / (Al * Bpl - Apl * Bl);
          
    return  PointAtParameter(line2D, t1);
}