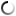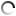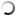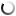Description
Backtracking is a general algorithm to finding all solutions for a computational problem. It’s used in solving constraint satisfactions problems.
The N-queens problems is about placing N queens on an NxN chess board so that no queen would be a threat to another.
Functions Used
There are 2 main methods I used to determine this. One determines if a queen is safe to be placed on a certain row and the other handles backtracking
//Testing if it's safe to place the queen
private bool IsSafe(char[,] Board, int row, int column)
{
//is column not safe - if for any other row on the same
//column we have a queen that it's not safe
for (int i = 0; i < row; i++) {
if (Board[i, column] == 'Q') return false; } //testing for the same \ diagonal
for (int i = row, j = column; i >= 0 && j >= 0; i--, j--)
{
if (Board[i, j] == 'Q') return false;
}
//testing for the same / diagonal
for (int i = row, j = column; i >= 0 && j < Size; i--, j++)
{
if (Board[i, j] == 'Q') return false;
}
return true;
}
private void Solve(char[,] Board, int row, int column)
{
if (column == 0 && row == Size)
{
this.Solutions.Add(CloneBoard(Board));
return;
}
for (int i = 0; i < Size; i++)
{
if (IsSafe(Board, row, i))
{
Board[row, i] = 'Q';
Solve(CloneBoard(Board), row + 1, 0);
Board[row, i] = '-';
}
}
}
Complete Solution
The solution defines a class that stores all the solutions in a List of matrix char. Queens will have the char ‘Q’ and empty items will have the char ‘-‘
public class NQueens
{
//the size of the board
public int Size { get; }
//A list to place all solutions
public List<char[,]> Solutions { get; }
//counting no of solutions
public int SolutionsCount => Solutions.Count();
public NQueens(int size)
{
this.Size = size;
this.Solutions = new List<char[,]>();
}
public void SolveNQueens()
{
char[,] board = new char[8, 8];
for (int i = 0; i < 8; i++)
{
for (int j = 0; j < 8; j++)
{
board[i, j] = '-';
}
}
Solve(board, 0, 0);
}
public void PrintSolution(int index)
{
StringBuilder sb = new StringBuilder();
for (int i = 0; i < Size; i++)
{
for (int j = 0; j < Size; j++)
{
sb.Append(Solutions[index][i, j]);
sb.Append(' ');
}
sb.AppendLine();
}
Console.Write(sb.ToString());
}
//Testing if it's safe to place the queen
private bool IsSafe(char[,] Board, int row, int column)
{
//is column not safe - if for any other row on the same
//column we have a queen that it's not safe
for (int i = 0; i < row; i++)
{
if (Board[i, column] == 'Q') return false; } //testing for the same \ diagonal
for (int i = row, j = column; i >= 0 && j >= 0; i--, j--)
{
if (Board[i, j] == 'Q') return false;
}
//testing for the same / diagonal
for (int i = row, j = column; i >= 0 && j < Size; i--, j++)
{
if (Board[i, j] == 'Q') return false;
}
return true;
}
private char[,] CloneBoard(char[,] board)
{
char[,] newBoard = new char[Size, Size];
for (int i = 0; i < Size; i++)
{
for (int j = 0; j < Size; j++)
{
newBoard[i, j] = board[i, j];
}
}
return newBoard;
}
private void Solve(char[,] Board, int row, int column)
{
if (column == 0 && row == Size)
{
this.Solutions.Add(CloneBoard(Board));
return;
}
for (int i = 0; i < Size; i++)
{
if (IsSafe(Board, row, i))
{
Board[row, i] = 'Q';
Solve(CloneBoard(Board), row + 1, 0);
Board[row, i] = '-';
}
}
}
}
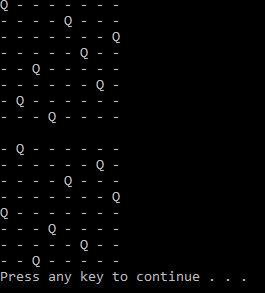
Console Application and WPF Preview
NQueens nQueens = new NQueens(8);
nQueens.SolveNQueens();
nQueens.PrintSolution(0);
Console.WriteLine();
nQueens.PrintSolution(10);